原文链接:第二章 马尔可夫决策过程 (MDP) (datawhalechina.github.io)
马尔可夫奖励过程(Markov reward process, MRP)是马尔可夫链加上奖励函数。在马尔可夫奖励过程中,状态转移矩阵和状态都与马尔可夫链一样,只是多了奖励函数(reward function)。奖励函数 R 是一个期望,表示当我们到达某一个状态的时候,可以获得多大的奖励。这里另外定义了折扣因子 γ 。如果状态数是有限的,那么 R 可以是一个向量。
回报与价值函数
这里我们进一步定义一些概念。范围(horizon) 是指一个回合的长度(每个回合最大的时间步数),它是由有限个步数决定的。 回报(return)可以定义为奖励的逐步叠加,假设时刻 t 后的奖励序列为 rt+1,rt+2,rt+3,⋯ 则回报为
Gt=rt+1+γrt+2+γ2rt+3+γ3rt+4+…+γT−t−1rT
其中,T是最终时刻,γ 是折扣因子,越往后得到的奖励,折扣越多。这说明我们更希望得到现有的奖励,对未来的奖励要打折扣。当我们有了回报之后,就可以定义状态的价值了,就是状态价值函数(state-value function)。对于马尔可夫奖励过程,状态价值函数被定义成回报的期望,即
Vt(s)=E[Gt∣st=s]=E[rt+1+γrt+2+γ2rt+3+…+γT−t−1rT∣st=s]
其中,Gt 是之前定义的折扣回报(discounted return)。我们对Gt取了一个期望,期望就是从这个状态开始,我们可能获得多大的价值。所以期望也可以看成未来可能获得奖励的当前价值的表现,就是当我们进入某一个状态后,我们现在有多大的价值。
我们使用折扣因子的原因如下。第一,有些马尔可夫过程是带环的,它并不会终结,我们想避免无穷的奖励。第二,我们并不能建立完美的模拟环境的模型,我们对未来的评估不一定是准确的,我们不一定完全信任模型,因为这种不确定性,所以我们对未来的评估增加一个折扣。我们想把这个不确定性表示出来,希望尽可能快地得到奖励,而不是在未来某一个点得到奖励。第三,如果奖励是有实际价值的,我们可能更希望立刻就得到奖励,而不是后面再得到奖励(现在的钱比以后的钱更有价值)。最后,我们也更想得到即时奖励。有些时候可以把折扣因子设为 0(γ=0),我们就只关注当前的奖励。我们也可以把折扣因子设为 1(γ=1),对未来的奖励并没有打折扣,未来获得的奖励与当前获得的奖励是一样的。折扣因子可以作为强化学习智能体的一个超参数(hyperparameter)来进行调整,通过调整折扣因子,我们可以得到不同动作的智能体。
在马尔可夫奖励过程里面,我们如何计算价值呢?如图 2.4 所示,马尔可夫奖励过程依旧是状态转移,其奖励函数可以定义为:智能体进入第一个状态 s1 的时候会得到 5 的奖励,进入第七个状态 s7 的时候会得到 10 的奖励,进入其他状态都没有奖励。我们可以用向量来表示奖励函数,即
R=[5,0,0,0,0,0,10]
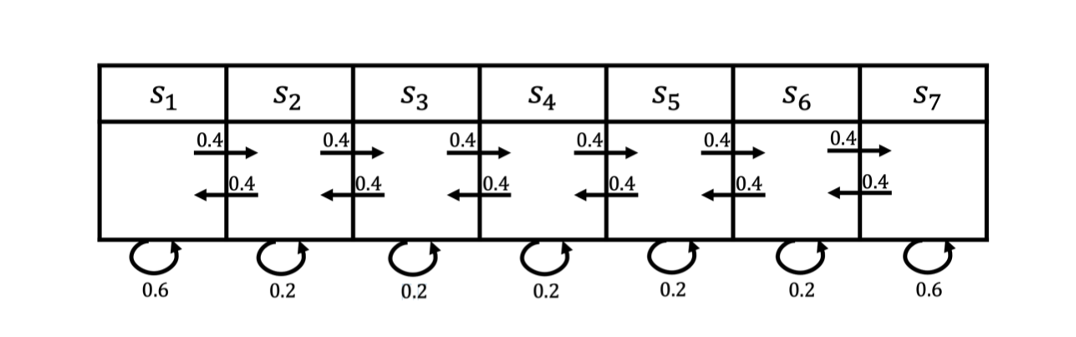
图 马尔可夫奖励过程的例子
我们对 4 步的回合(γ=0.5)来采样回报 G。
(1)s4,s5,s6,s7的回报:0+0.5×0+0.25×0+0.125×10=1.25
(2)s4,s3,s2,s1的回报:0+0.5×0+0.25×0+0.125×5=0.625
(3)s4,s5,s6,s6的回报:0+0.5×0+0.25×0+0.125×0=0
我们现在可以计算每一个轨迹得到的奖励,比如我们对轨迹 s4,s5,s6,s7 的奖励进行计算,这里折扣因子是 0.5。在 s4 的时候,奖励为0。下一个状态 s5 的时候,因为我们已经到了下一步,所以要把 s5 进行折扣,s5 的奖励也是0。然后是 s6,奖励也是0,折扣因子应该是0.25。到达 s7 后,我们获得了一个奖励,但是因为状态 s7 的奖励是未来才获得的奖励,所以我们要对之进行3次折扣。最终这个轨迹的回报就是 1.25。类似地,我们可以得到其他轨迹的回报。
这里就引出了一个问题,当我们有了一些轨迹的实际回报时,怎么计算它的价值函数呢?比如我们想知道 s4 的价值,即当我们进入 s4 后,它的价值到底如何?一个可行的做法就是我们可以生成很多轨迹,然后把轨迹都叠加起来。比如我们可以从 s4 开始,采样生成很多轨迹,把这些轨迹的回报都计算出来,然后将其取平均值作为我们进入 s4 的价值。这其实是一种计算价值函数的办法,也就是通过蒙特卡洛(Monte Carlo,MC)采样的方法计算 s4 的价值。


